Process improvement initiatives in mineral processing plants will typically culminate in some type of a plant trial, where the effect of the change (reagent, process control, equipment or technology, etc.) is tested in a full-scale production environment. Most metallurgists will, at some point in their early careers, learn the hard way that these types of experiments are very different to their laboratory-based analogues, in that the prevailing conditions of the production plant are difficult to hold constant. Unlike laboratory experiments, in which process variables can be closely controlled, plant trials are subject to largely uncontrollable changes in variables such as throughput, ore mineralogy, and operator practice, leading to unplanned variations in daily concentrator performance during, and even prior to, the commencement of the trial.
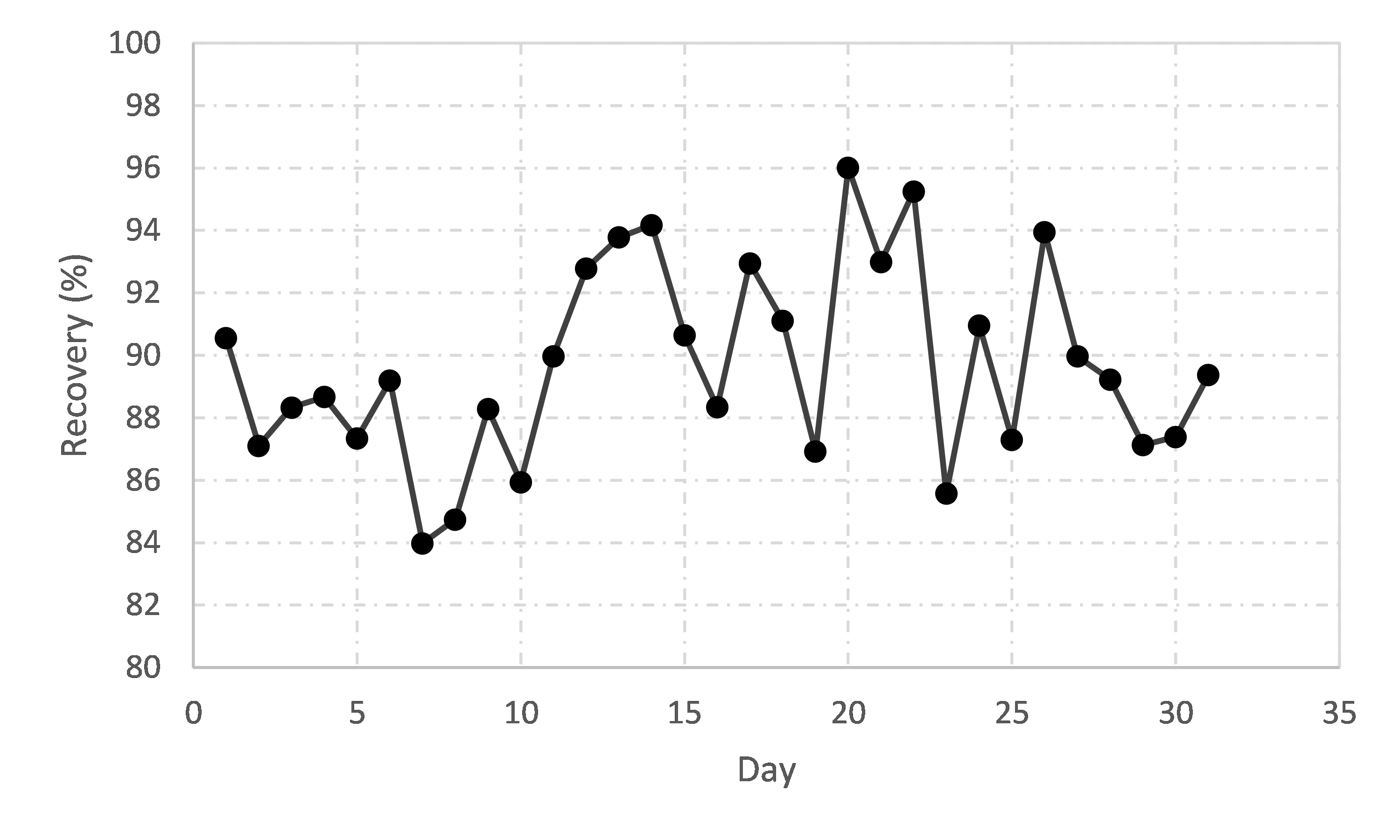
Such variability will usually camouflage any real effects of a tested change, and in so doing, exacerbate the risks of poor decision-making after the trial has ended. Given that implementing changes often entails increased costs, whether in higher OPEX, CAPEX (or both), one of the key objectives of plant trials is to mitigate the risks of proceeding with changes that not only are potentially expensive, but could also lead to no benefit or could perhaps even be detrimental to overall performance. The problem confronting production metallurgists is that, if a change has the potential to improve circuit performance by (say) 2% - a magnitude typical of optimisation efforts and often worth millions of dollars per year in extra metal production – how can one know whether or not the tested change has ‘worked’, especially when the range of day-to-day concentrator performance can be in the order of 10-20%, as in Figure 1?
The answer, perhaps surprisingly, is ‘easily’, with the correct experimental design, followed by analysis using robust statistical methodologies. There are a range of experimental designs to choose from, depending on the context and the objectives of the experiment, with many discussed in mineral processing literature. Common to these experiments is in the ability of the ensuing analysis to disentangle the effect of the trial variable(s) from the effect of interfering variables and background experimental error (‘noise’). Such experiments circumvent the problems of uncontrollable production variables swamping the effect of the trial variable. However, a key requirement is adherence to the statistical criteria underlying the experimental designs.
For the common case of comparing two conditions (e.g. new vs. old reagent, equipment ON vs. equipment OFF), the best type of experiment is the paired trial. This type of experimental design has become ubiquitous in mineral processing, as the resulting data is compatible with the paired t-test, a simple yet powerful analytical procedure that can detect small differences in seemingly overwhelming noise.
However, the design of an appropriate paired trial can sometimes prescribe durations that are quite long in order to control the risks of incorrect decision making. There is often a temptation to terminate a trial as soon as a desired result is observed; however, implicit in the paired t-test approach is that the sample size is large enough for its outputs to be meaningful. An alternative to conventional t-testing is sequential t-testing, which can alleviate sample size requirements, and will indicate whether a trial can be terminated earlier than expected.
Sequential testing is not a new concept; it was developed in the 1940s as part of wartime efforts to improve Allied industrial productivity. It initially found application in manufacturing but has since been applied to other disciplines such as forestry, psychology, and clinical monitoring. Details of the calculation approach are described in Vizcarra et al. (2023); as results are collected, they are transformed into a likelihood ratio (LR) which can be trended in real-time. If the LR crosses either an upper or lower boundary (defined by the experimenters’ risk tolerance for making incorrect decisions), then the trial can be terminated. This often leads to a shorter trial than what would be prescribed with a conventional paired-trial design.
An example is shown in Figure 2a, which is the LR trend from an ON/OFF trial of a flash flotation cell in a Pb/Zn concentrator. The trial could have terminated after 14 pairs with 95% confidence of a real recovery improvement (1.4 +/- 1.1%, Figure 2b). This compares to n = 27 calculated by the classical sample size formula, a ~50% reduction in required sample size.
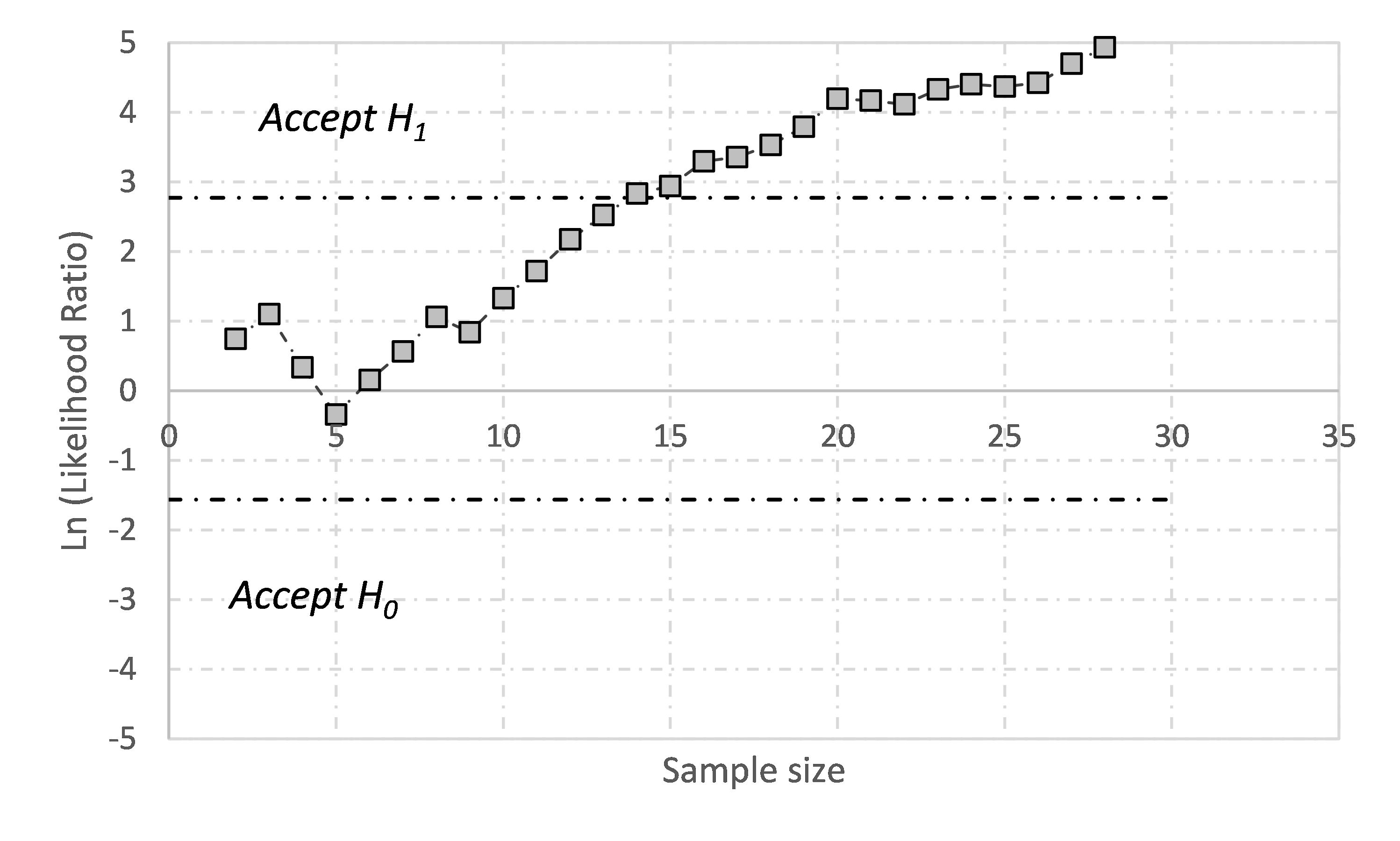
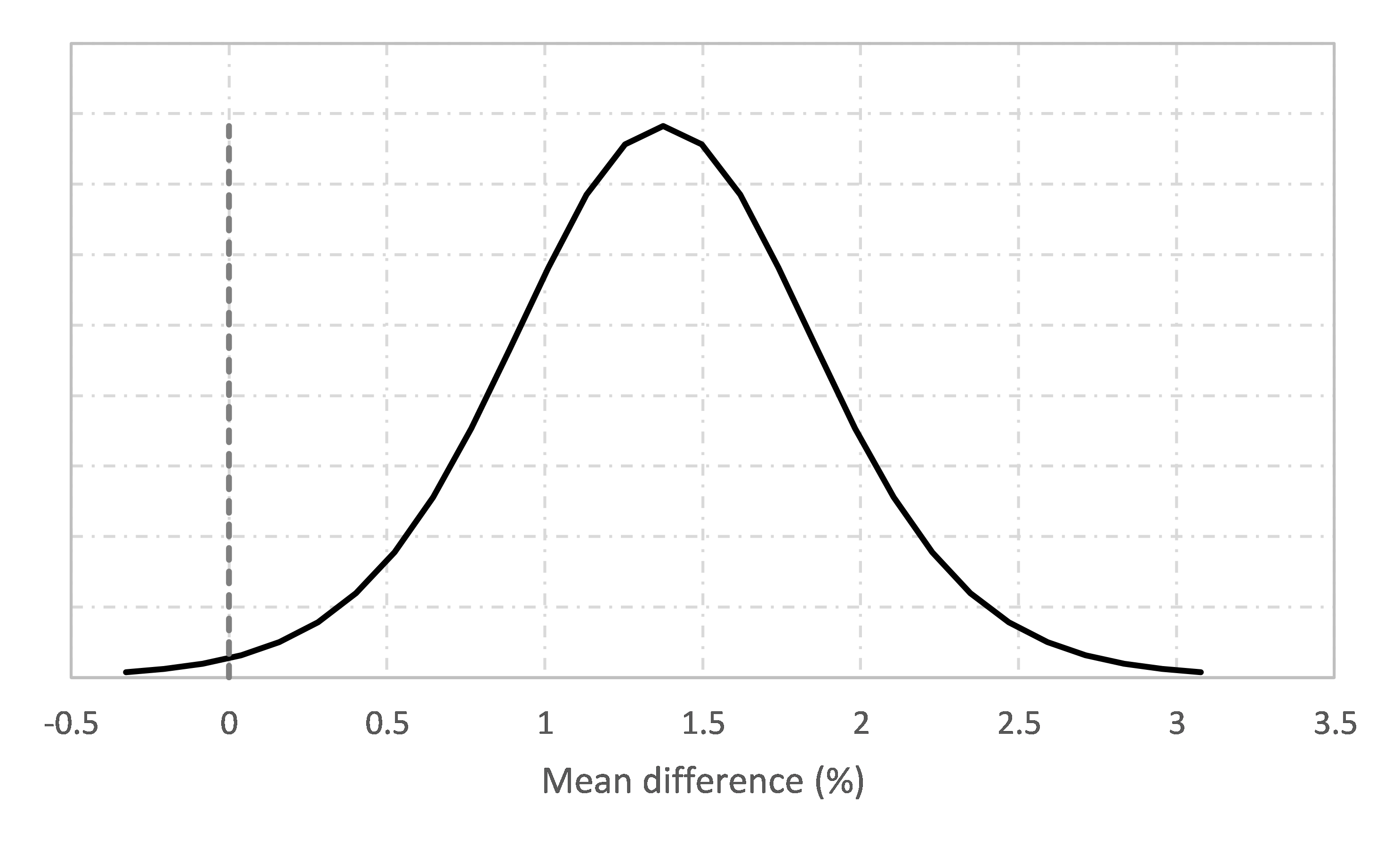
recovery improvement (reference line =0%)
JKTech has many other case studies of where sequential testing has reduced trial durations by typically ~30-50%, compared to what has been prescribed by traditional sample size formulas. Sequential testing is now the approach of choice when JKTech designs full-scale plant trials. These case studies, and more details of the sequential testing method, can be found in Vizcarra et al. (2023).
One of JKTech’s flagship professional development courses, Comparative Statistics and Experimental Design for Mineral Engineers, is delivered regularly, both online and in-person. For more information, contact training@jktech.com.au
References
Vizcarra, T.G., Napier-Munn, T.J., Felipe, D., 2023. Sequential t-testing in Plant Trials - A Faster Way to the Answer, MetPlant, Adelaide.